Crystal structure

Crystal structures are periodic arrangements of atoms in 3D space, serving as the source codes for diverse materials, such as permanent magnets, battery materials, and superconductors.

A crystal structure is typically described by its repeatable 3D slice called a unit cell. We assume a unit cell consisting of $N$ atoms and denote it as $(A, P, L)$:

• $A = [a_1, a_2, \cdots, a_N] \in \mathbb{N}^{1 \times N}$: the species (atomic numbers) of unit cell atoms.
• $P = [\bm{p}_1, \bm{p}_2, \cdots, \bm{p}_N] \in \mathbb{R}^{3 \times N}$: the 3D Cartesian coordinates of unit cell atoms.
• $L = [\bm{\ell}_1, \bm{\ell}_2, \bm{\ell}_3] \in \mathbb{R}^{3 \times 3}$: lattice vectors that define periodic unit-cell translations in 3D space.

By tiling the unit cell to fill 3D space, the species and positions of atoms in the crystal structure are determined as follows.

$$\begin{align*}\hat{A} &= \{a_{i(\bm{n})} | a_{i(\bm{n})}=a_i, \bm{n}\in\mathbb{Z}^3, 1\leq i \leq N\}\\ \hat{P} &= \{\bm{p}_{i(\bm{n})} | \bm{p}_{i(\bm{n})}=\bm{p}_i+L\bm{n}, \bm{n}\in\mathbb{Z}^3, 1\leq i \leq N\}\end{align*}$$

Here, we use $i$ to denote the $i$ -th atom in the unit cell, and use $i(\bm{n})$ to denote its duplicate by the 3D translation: $L\bm{n} = n_1\bm{\ell}_1 + n_2\bm{\ell}_2 + n_3\bm{\ell}_3$. We use $j$ and $j(\bm{n})$ similarly.

SE(3)-invariant structural modeling

We consider the problem of estimating the physical state of a given crystal structure, assuming that the state remains invariant under rigid transformations (i.e., rotations and translations). Such a state typically corresponds to material properties, such as formation energy and bandgap.

We represent the state of a crystal structure by a set of abstract atom-wise state features for the unit-cell atoms:

$$X = [\bm{x}_1, \bm{x}_2, \cdots, \bm{x}_N] \in \mathbb{R}^{d \times N}.$$

As input to a graph neural network (GNN), these features are usually initialized via atom embeddings:

$$X^{(0)} \gets \text{AtomEmbedding}(A),$$

which only symbolically represent atomic species. They are then evolved through message-passing layers

$$X^{(t+1)} \gets f^{(t)}(X^{(t)}, P, L)$$

to eventually reflect the atomic states appropriate for a target task.

Challenges in SE(3)-invariant GNNs

There are several approaches to ensuring SE(3) invariance in GNNs:

• Invariant features: Leveraging inherently invariant geometric features, such as interatomic distances $\|\bm{p}_j - \bm{p}_i\|$ and angles between triplets $\cos(\bm{p}_j - \bm{p}_i, \bm{p}_k - \bm{p}_i)$, ensures SE(3) invariance. However, fully distance-based models have limited expressive power, and incorporating three-body interactions significantly increases computational complexity.
• Frames: Another straightforward approach is to standardize the orientation of a given structure through a structure-aligned coordinate system called a frame. However, determining frames for crystal structures is challenging due to their infinite and highly symmetric nature.

We explore a new frame-based methodology to incorporate richer yet invariant structural information beyond distances.

What is the role of frames?

Surely, it is to standardize the orientations of given structures so that GNN models can directly exploit 3D coordinate information as invariant geometric features.

―― Is that all?

Let’s dig deeper into how frames work in a GNN, whose message-passing layers are assumed to include the following general operation:

$$\bm{x}'_i = \sum_{j=1}^{N} \sum_{\bm{n}\in \mathbb{Z}^3} \,\, \underbrace{w_{ij(\bm{n})}}_{\text{Weight}} \,\, \underbrace{\bm{f}_{i\gets j(\bm{n})}(\bm{x}_{j(\bm{n})}, \hat{P})}_{\text{Message}}.$$

This equation describes that the state $\bm{x}$ of each unit-cell atom $i$ is updated by receiving abstract influences or ‟messages”, $\bm{f}_{i\gets j(\bm{n})}$, from atoms $j(\bm{n})$ in the structure, weighted by scalars $w_{ij(\bm{n})}$. In recent transformer models, these weights are determined dynamically via self-attention mechanisms.

Distance-based GNNs ensure SE(3) invariance by simply formulating $\bm{f}_{i\gets j(\bm{n})}$ with the interatomic distance, $r_{ij(\bm{n})} = \|\bm{p}_{j(\bm{n})} - \bm{p}_i \|$, as follows:

$$\bm{f}^{\text{dist}}_{i\gets j(\bm{n})}(\bm{x}_{j(\bm{n})}, \hat{P}) := \bm{h}_{i\gets j(\bm{n})}(\bm{x}_{j(\bm{n})}, r_{ij(\bm{n})} ).$$

The role of frames is to offer, for the design of the message function $\bm{f}_{i\gets j(\bm{n})}$, more informative invariant features beyond the distance through a structure-aligned coordinate system $F \in \mathbb{R}^{3 \times 3}$, as follows:

$$\bm{f}^{\text{frame}}_{i\gets j(\bm{n})}(\bm{x}_{j(\bm{n})}, \hat{P}) := \bm{h}_{i\gets j(\bm{n})}(\bm{x}_{j(\bm{n})}, r_{ij(\bm{n})}, F\bm{r}_{ij(\bm{n})} ),$$

where the frame-projected relative position $F\bm{r}_{ij(\bm{n})}$ remains invariant under global rotations and translations for the crystal structure $\hat{P}$.

Dynamic frames

Given that the end-users of frames are the message functions $\bm{f}_{i\gets j(\bm{n})}$ in GNNs, shouldn't we tailor a frame for each message function in each layer so that the function receives a better-normalized structure?

―― We pursue this idea by introducing the concept of dynamic frames.

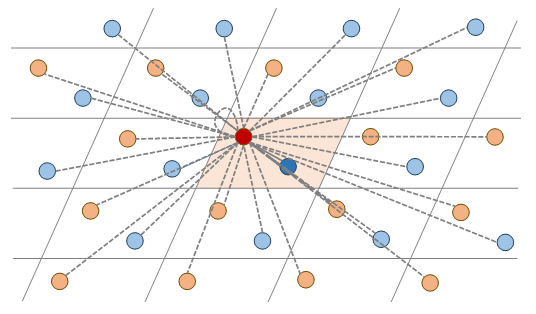
In each message passing layer, the target atom $i$ receives more influences from atoms $j(\bm{n})$ with larger weights $w_{ij(\bm{n})}$, and no influence from atoms $j(\bm{n})$ with zero weights. This means that, when updating the state of atom $i$, this atom has its own partial and local view of the structure $\hat{P}$ through weights $w_{ij(\bm{n})}$ acting as a mask on the structure.

As a dynamic frame, we therefore construct an atom-wise frame $F_i$ for each target atom $i$ by using this masked view of the structure $\hat{P}$ with weights $\bm{w}_{i}$, as follows:

$$F_i \gets \text{FrameConstruction}_i(\hat{P}, \bm{w}_{i}).$$

Typically, we define an orthonormal basis $F_i = [\bm{e}_1, \bm{e}_2, \bm{e}_3]^T$ as a frame, where the first and second axes point towards the primary and secondary influential directions of interatomic interactions. (See the paper for detailed definitions.)

This dynamic frame is then used to project the relative position vectors $\bm{r}_{ij(\bm{n})}$ in order to derive the messages for the target atom $i$, as follows:

$$\bm{f}^{\text{dynamic}}_{i\gets j(\bm{n})}(\bm{x}_{j(\bm{n})}, \hat{P}) := \bm{h}_{i\gets j(\bm{n})}(\bm{x}_{j(\bm{n})}, r_{ij(\bm{n})}, F_i \bm{r}_{ij(\bm{n})} ).$$

Importantly, our dynamic frames are constructed with the entire structure $\hat{P}$, rather than with a specific unit-cell representation $(P, L)$. Thus, our dynamic frames are invariant under the unit-cell variations within the same crystal structure.

We demonstrate the proposed concept of dynamic frames by utilizing the Crystalformer architecture (Taniai et al., ICLR 2024). Crystalformer employs the standard softmax self-attention for message passing, which is formulated as infinitely connected distance-decay attention as follows:

$$\begin{align*}\bm{x}'_i &= \sum_{j=1}^{N} \sum_{\bm{n}\in \mathbb{Z}^3} \color{#C00000} \,\, w_{ij(\bm{n})} \,\, \color{#0070C0} \bm{f}_{i\gets j(\bm{n})}(\bm{x}_{j(\bm{n})}, \hat{P}) \\ &= \sum_{j=1}^N\sum_{\bm{n}\in \mathbb{Z}^3} \color{#C00000} {\frac{1}{Z_i} \exp\left(\frac{{\bm{q}_i^T \bm{k}_{j}}}{\sqrt{d_K}} - \frac{\|\bm{r}_{ij(\bm{n})}\|^2}{2\sigma_i^2}\right)} \color{#0070C0} {\left(\bm{v}_{j} +\bm{\psi}_{ij(\bm{n})}\right)}.\end{align*}$$

Here, query $\bm{q}$, key $\bm{k}$, and value $\bm{v}$ are linear projections of the current state $\bm{x}$. Scalar $Z_i$ is the normalizer of softmax attention weights. Vector $\bm{\psi}_{ij(\bm{n})}$ is a geometric relative position encoding for atoms $i$ and $j(\bm{n})$.

Originally, $\bm{\psi}_{ij(\bm{n})}$ simply encodes the scalar distance $r_{ij(\bm{n})}$ via a linear projection of Gaussian basis functions (GBFs). In this work, we enhance the model's expressive power by incorporating frame-based geometric features into the Crystalformer's relative position encoding $\bm{\psi}_{ij(\bm{n})}$. This results in a new architecture CrystalFramer.

Frame-based invariant features

Given the unit direction vector $\bar{\bm{r}}_{ij(\bm{n})} = \bm{r}_{ij(\bm{n})} / r_{ij(\bm{n})}$, we obtain its invariant representation $\bm{\theta}_{ij(\bm{n})} = F_i \bar{\bm{r}}_{ij(\bm{n})}$, where the $k$ -th component represents the cosine of the angle between the $k$ -th axis and the direction:

$$\theta_{ij(\bm{n})}^{(k)} = \bm{e}_k \cdot \bar{\bm{r}}_{ij(\bm{n})}.$$

Using GBFs $\bm{b}(x)$ as a mapping from a scalar to a vector, we linearly combine the distance-based and three angle-based edge features, as follows:

$$\bm{\psi}_{ij(\bm{n})} = W_0 \bm{b}_\text{dist}\left(r_{ij(\bm{n})}\right) + \sum_{k=1,2,3} W_k\bm{b}_\text{angl}\left(\theta_{ij(\bm{n})}^{(k)}\right).$$

This $\bm{\psi}_{ij(\bm{n})}$ as a whole essentially encodes the 3D relative position vector, $\bm{r}_{ij(\bm{n})} = \bm{p}_{j(\bm{n})} - \bm{p}_i$.

Architecture

Below is the architecture of CrystalFramer, where we have introduced dynamic frame construction and frame-based edge features, as highlighted in the figure.

Given the multi-head self-attention mechanism, we dynamically construct a frame for each target atom, head, and layer during the self-attention operation.

We evaluated the performance of CrystalFramer using two types of dynamic frames: weighted PCA frames and max frames. We compared these with existing crystal frames (PCA frames and lattice frames) and other state-of-the-art crystal encoders. For evaluation, we used three datasets: JARVIS (55,723 materials), Materials Project (69,239 materials), and OQMD (817,636 materials).

JARVIS dataset

Materials Project dataset

OQMD dataset

Overall, CrystalFramer significantly improves the baseline performance of CrystalFormer and outperforms most existing methods across various tasks and datasets.

Max frames capture local motiffs around the target atom, while weighted PCA frames look at the structure over broader areas. Both types of frames tend to focus on close neighbors in shallow layers and relatively distant neighbors in deeper layers.